You know how certain events in life tend to trigger a chain reaction? For instance, think about when one person starts a rumor in a small town—suddenly, everyone is talking about it. Well, Hawkes Processes behave in a similar way, mathematically speaking.
A Hawkes Process is what we call a self-exciting point process. This simply means that the occurrence of an event increases the probability of future events happening soon after. Unlike a Poisson process, where events happen independently over time, in a Hawkes process, each event can “trigger” or “excite” subsequent events. It’s like tossing a pebble into a pond—one event creates ripples that continue to influence the system for a while.
Now, you might be wondering: Why does this matter? Here’s the deal—Hawkes processes are widely used in fields that require the modeling of event clustering or bursts of activity. For example, in finance, you might model how trades in the stock market are not random, but rather how one trade can cause a chain of reactions, leading to more trades. In seismology, after an earthquake, aftershocks tend to follow in rapid succession, and this “self-exciting” nature is exactly what Hawkes Processes model.
So, in a nutshell, Hawkes Processes help us understand and predict how events—whether financial trades, social media posts, or earthquakes—cause further activity, often in a ripple-like manner.
Use Cases:
Let’s get into the real-world applications to make this more concrete. Imagine you’re analyzing how information spreads on social media. One person tweets, and soon their followers are retweeting it, leading to a cascade of retweets, likes, and comments. A Hawkes Process could model this pattern, helping you predict when and how often people will engage with the tweet.
In seismology, the clustering of earthquakes is another classic example. When a large earthquake occurs, aftershocks are likely to follow in waves. The Hawkes process allows seismologists to forecast the likelihood of these aftershocks, improving their ability to issue warnings.
And don’t forget finance. In the stock market, a trade by a major player often triggers a flurry of activity. Other traders react to the initial trade, leading to bursts of subsequent trades—this is exactly what the self-exciting nature of a Hawkes Process captures.
In all these cases, what’s fascinating about Hawkes Processes is their ability to help you model “triggering” behavior, where one event sets off a series of related events. It’s almost like they capture the hidden dynamics of real-world interactions that would otherwise appear random.
Excitation Kernels
Types of Kernels:
Now, let’s dive into the excitation kernels—the heart of what drives the self-exciting behavior in a Hawkes Process. Think of kernels like “reaction functions” that determine how much influence an event has on future events.
There are different types of kernels, and the one you choose depends on what kind of process you’re modeling. The most common types are:
- Exponential kernels: These are the workhorse of Hawkes Processes. They model how the effect of an event decays over time, like how excitement about a tweet fades after a few hours. The formula might look something like this:ϕ(t)=αe−βt\phi(t) = \alpha e^{-\beta t}ϕ(t)=αe−βtwhere α\alphaα controls the size of the influence, and β\betaβ controls how fast it decays.
- Power-law kernels: These are used when the influence of an event decays more slowly over time. Imagine aftershocks from an earthquake that continue to happen even days later—that’s where power-law kernels shine.
Impact on Event Dynamics:
You might be asking, Why should I care about different kernels? Here’s why: the type of kernel directly impacts the clustering behavior of events. An exponential kernel, for example, makes future events less likely as time goes on, meaning events cluster tightly together right after a triggering event. This might be perfect if you’re modeling something like high-frequency financial trades that happen in rapid succession, but then taper off.
On the other hand, power-law kernels are useful when you need to capture events that continue to have long-lasting effects. For example, in seismology, aftershocks can continue for weeks or even months after the main event. The power-law kernel captures this slow decay, making it ideal for such processes.
To give you a clearer picture, let’s take social media as an example. If you’re modeling how a viral video sparks engagement, you might want to use an exponential kernel since most interactions—likes, shares, and comments—happen within the first 24 hours. But if you’re studying something with a longer tail—like news articles that stay relevant for weeks—you might opt for a power-law kernel.
Choosing the right kernel is crucial because it directly determines how well your model reflects reality. The wrong kernel could lead to poor predictions or a misunderstanding of how events really interact in your system.
Conditional Intensity and Likelihood Estimation
Conditional Intensity:
Let’s start with something that forms the backbone of the Hawkes Process: conditional intensity. You might be wondering, What does this actually mean in plain terms? Well, imagine you’re trying to predict when the next earthquake will hit after a major quake. Conditional intensity is the mathematical tool that helps you figure out how likely future events are, given all the events that have already happened.
In more technical terms, the conditional intensity function is a time-dependent rate, λ(t)\lambda(t)λ(t), that tells you the probability of an event occurring at a given moment in time, based on past events. The cool part? It’s not static. It updates as new events happen, meaning it’s constantly recalculating the likelihood of future events.
Think of it like this: if you’re monitoring financial transactions, and a sudden flurry of trades happens, the conditional intensity would spike, suggesting that more trades are likely to follow in the near future. It’s like the model is constantly looking over its shoulder, taking into account what has just happened to predict what will happen next. This makes it a dynamic model, perfectly suited for scenarios where events tend to cluster together over time.
Maximum Likelihood Estimation (MLE):
Now, how do we get a model that can accurately predict future events? Here’s where Maximum Likelihood Estimation (MLE) comes in. MLE is a statistical method that helps you estimate the parameters of the Hawkes Process—things like the baseline intensity μ\muμ and the triggering function ϕ(t)\phi(t)ϕ(t)—so that the model best fits the observed data.
Here’s the deal: MLE works by finding the set of parameters that make the observed sequence of events most probable under the model. Imagine you’re tuning a guitar—MLE is like adjusting the tension of the strings until you get just the right sound. In the case of Hawkes Processes, it adjusts the parameters until the model best matches the real-world event patterns you’re observing.
To put it simply, MLE helps you ‘train’ your Hawkes model on data, just like how you would train a machine learning model. And once you have those optimal parameters, the model becomes much better at predicting future events because it reflects the dynamics of your data more accurately.
Alternative Estimation Methods:
MLE isn’t the only game in town. While it’s often the go-to method, there are other techniques you can use to estimate parameters, especially when the data or the model gets more complicated.
One of the alternatives is Bayesian Inference. You might have heard of Bayesian methods as a way of incorporating prior knowledge into your model. In the context of Hawkes Processes, Bayesian inference can help you estimate parameters by combining the observed data with prior beliefs about what those parameters should be. This can be especially useful if you’re dealing with noisy data or have limited observations.
There are also other methods like variational inference and expectation-maximization, but MLE and Bayesian inference are the most commonly used when it comes to Hawkes Processes. These alternatives might come in handy depending on the complexity of your data and the trade-offs you’re willing to make in terms of computational cost.
Multivariate Hawkes Processes
Introduction to Multivariate Extensions:
You might be thinking, Is there more to Hawkes Processes? Well, yes! What we’ve discussed so far deals with a single event type, like the spread of information on Twitter or aftershocks in seismology. But real-world systems are often more complex, involving multiple types of events that interact with each other. That’s where Multivariate Hawkes Processes come into play.
A Multivariate Hawkes Process allows you to model different types of events that can either excite themselves or each other. For example, let’s say you’re analyzing crime data. You might have different types of crimes—burglaries, assaults, and vandalism—that tend to cluster together in certain neighborhoods. A burglary might make an assault more likely, or a vandalism event could trigger more of the same.
What’s amazing here is that the self-exciting nature of Hawkes processes can now extend across different types of events. You’re no longer confined to looking at one type of event in isolation. Instead, you’re capturing the complex web of interactions between various event types.
Cross-excitation:
Now let’s talk about the concept of cross-excitation—it’s a powerful way to capture how one event type can influence another. You can think of it like how a wildfire spreads: a small spark might ignite one tree, but soon the flames are jumping from tree to tree, creating a massive blaze. In the same way, cross-excitation models how an event of one type can “ignite” a different type of event.
Take financial markets as an example. A large trade in one stock might trigger trades in other related stocks. Or imagine in social networks, where a tweet on a trending topic could lead not only to more tweets but also to blog posts or news articles on the same topic. Cross-excitation helps you capture these complex interdependencies in a mathematically rigorous way.
In a multivariate setting, the intensity function λ(t)\lambda(t)λ(t) for each event type gets an additional term that accounts for the impact of other event types. This means the model not only looks at the history of its own events but also takes into account events of different types, giving you a more comprehensive understanding of how events interact in your system.
Let’s not forget that in fields like epidemiology, cross-excitation is key. The spread of a disease in one region could lead to outbreaks in neighboring areas, and a multivariate Hawkes model helps capture these spatial and temporal interactions.
Applications of Hawkes Processes
Social Networks:
Let’s start with something you’re probably already familiar with—social networks. You’ve likely noticed how one viral post or tweet spreads like wildfire, creating ripples of engagement. Retweets, likes, and shares don’t just happen randomly; one interaction often triggers more. This is where Hawkes Processes come into play. They model contagion on networks, helping you understand how one event leads to a cascade of reactions.
Imagine you tweet something. Your followers start retweeting, and their followers do the same. The key here is that each retweet increases the likelihood of further retweets, and Hawkes Processes capture this self-exciting behavior. They can help you predict how far and fast information will spread based on the initial burst of activity. This might surprise you: not only can they model this on an individual post level, but you can also use them to understand large-scale trends, like how news spreads or how memes go viral.
Financial Markets:
Now, let’s shift gears to financial markets. Imagine you’re monitoring high-frequency trading—those ultra-fast trades made by algorithms. In this setting, Hawkes Processes are crucial for modeling bursts of trading activity. Here’s how it works: one large trade can set off a flurry of smaller trades as other traders react. This chain reaction is exactly the kind of pattern Hawkes Processes excel at modeling.
You might be wondering, How does this help in the real world? Well, traders and analysts use Hawkes models to anticipate market volatility, such as during a market crash. When one stock price starts dropping rapidly, it often leads to a cascading effect where other stocks also plummet. By capturing these self-exciting patterns, Hawkes Processes can help model these crashes or predict periods of high activity, aiding risk management and trading strategies.
Seismology:
You’ve probably heard of aftershocks following a big earthquake. But did you know that Hawkes Processes are actually used to model these aftershocks? In seismology, events tend to cluster—after a major quake, there’s often a sequence of smaller quakes that follow. The self-exciting nature of the Hawkes Process makes it perfect for modeling these aftershocks.
Here’s the deal: seismologists use Hawkes models to estimate the probability of aftershocks after a main event. For instance, after a significant earthquake, a Hawkes model can predict when and how many aftershocks are likely to occur, giving seismologists valuable insights into seismic activity. And what’s really powerful is that they can do this in near real-time, helping to improve earthquake forecasting.
Epidemiology:
You might not have expected this, but epidemiology is another field where Hawkes Processes have proven invaluable. Think about how a disease spreads through a population—it doesn’t just happen at random. One infected individual tends to infect others, creating a chain reaction. Hawkes Processes are now being used to model this self-exciting spread of diseases, particularly in understanding outbreaks.
For example, during an epidemic, you can use a Hawkes Process to model how each new case increases the likelihood of further cases in nearby areas. This can be incredibly useful in public health planning, allowing authorities to predict where new outbreaks are likely to occur and take preemptive action.
Simulating Hawkes Processes
Simulation Methods:
So now that you’ve got a good understanding of how Hawkes Processes work, you might be wondering, How do we actually simulate these processes? One of the most common methods used to simulate events in a Hawkes Process is Ogata’s thinning algorithm.
Here’s how it works in a nutshell: Ogata’s algorithm allows you to simulate the occurrence of events over time by using the conditional intensity function λ(t) to decide whether or not an event happens. Think of it like a filter—it “thins” out the timeline by determining where events should fall based on their intensity.
First, you generate candidate times for events from a Poisson process, which is the base for a Hawkes Process. Then, using the conditional intensity, you decide whether to keep or discard each candidate event. The algorithm repeats this process until you’ve generated a full timeline of events, with the events clustering in a way that reflects the self-exciting nature of the Hawkes Process.
Practical Example:
Let’s make this more concrete with a step-by-step example. Say we want to simulate a Hawkes Process using a simple exponential kernel. Here’s what you’d do:
- Set the baseline intensity (μ)—this is the probability of an event happening on its own, without being triggered by previous events.
- Define the excitation function (ϕ(t))—let’s use an exponential decay function here to model how the effect of one event fades over time:
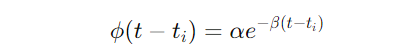
3. Simulate candidate events: Using a Poisson process, generate a list of potential events over the time period you’re interested in.
4. Apply thinning: For each candidate event, use the conditional intensity function to decide whether to keep the event or discard it. If the intensity is high (meaning many events have occurred recently), you’re more likely to keep the event.
5. Update the intensity: Each time you keep an event, update the intensity function for future events by adding the excitation caused by the new event.
By the end of this process, you’ll have a timeline of events that reflects the clustering behavior we see in real-world data. Whether you’re simulating tweets, trades, or earthquakes, Ogata’s algorithm allows you to reproduce the self-exciting patterns that are the hallmark of Hawkes Processes.
Software and Implementations
Popular Libraries:
You might be thinking, How can I actually implement Hawkes Processes in my own projects? Luckily, you don’t have to start from scratch! There are several powerful libraries that make working with Hawkes Processes easy, especially if you’re using Python.
- tick (Python): This is perhaps the most popular library for implementing Hawkes Processes. Not only does it allow you to simulate and estimate Hawkes models, but it also supports multivariate models. You can use
tickfor real-world applications like modeling financial trades or social media events. Its built-in support for exponential and power-law kernels gives you flexibility in modeling different types of self-exciting behavior.Here’s whytickis fantastic: it’s fast, thanks to its use of sparse arrays, and it’s equipped with robust tools for parameter estimation, like Maximum Likelihood Estimation (MLE). Whether you’re building a simple univariate model or a complex multivariate one,tickhas you covered. - hawkes (R): If you prefer working in R, the
hawkespackage is a go-to tool. It provides basic functionality for simulating Hawkes Processes, making it perfect for smaller projects or quick analyses. While it’s not as feature-rich astick, it’s a solid choice if you’re working within the R ecosystem. - statsmodels (Python): While not a dedicated library for Hawkes Processes,
statsmodelscan be helpful for preliminary analyses, especially when estimating parameters for point processes or conducting statistical modeling.
Now, you might be wondering, How do I get started with code? Let me walk you through a simple example using Python’s tick library.
Code Example:
Here’s a quick Python snippet to help you implement a univariate Hawkes process with an exponential kernel. This will give you a hands-on feel for how these processes work in practice.
# First, install the tick library if you don't have it
# pip install tick
import numpy as np
from tick.hawkes import SimuHawkesExpKernels
# Define the baseline intensity (mu) and the kernel parameters (alpha, beta)
mu = 0.5 # baseline intensity
alpha = 0.8 # self-excitation factor
beta = 1.5 # decay rate of the exponential kernel
# Initialize the Hawkes Process with an exponential kernel
hawkes = SimuHawkesExpKernels(adjacency=np.array([[alpha]]), decays=np.array([[beta]]), baseline=np.array([mu]), end_time=10)
# Simulate the Hawkes process over a period of 10 units of time
hawkes.simulate()
# Plot the event timeline
import matplotlib.pyplot as plt
hawkes.plot()
# Show the times of events
print("Event times:", hawkes.timestamps[0])
Here’s what’s happening in this code:
- μ sets the baseline intensity (how often events occur on their own).
- α controls how strongly each event excites future events.
- β is the rate at which the influence of each event decays over time.
When you run this, the hawkes.plot() function will generate a plot showing the times when events occurred, giving you a visual representation of how events cluster together in time. Try playing around with the parameters to see how changing α, μ, and β affects the behavior of the process.
This code provides a practical starting point, showing how easily you can simulate and visualize a Hawkes Process. Once you’ve got a handle on the basics, you can expand this to multivariate models or experiment with different kernels for more complex simulations.
Conclusion
By now, you’ve probably realized that Hawkes Processes are much more than just a mathematical curiosity—they’re an incredibly versatile tool for modeling self-exciting events in the real world. Whether you’re tracking the spread of information on social networks, modeling trades in financial markets, or predicting aftershocks after an earthquake, Hawkes Processes provide a powerful framework for understanding how events cluster and trigger one another over time.
Here’s the takeaway: Hawkes Processes capture the ripple effects of events. They help you understand why and how certain events lead to more events. If you’ve ever wondered how a viral tweet leads to a cascade of interactions, or how a single trade triggers a flurry of market activity, then you’ve just brushed the surface of what Hawkes Processes can do.
What makes them stand out is their ability to model self-excitation—the idea that one event doesn’t just happen in isolation, but actually increases the likelihood of future events. This is what sets Hawkes Processes apart from simpler models like Poisson processes, which assume events happen independently. In real life, things are often far more interconnected.
As you move forward, you’ll find that applications of Hawkes Processes are continuing to expand, from traditional areas like seismology to cutting-edge fields like epidemiology, cybersecurity, and even artificial intelligence. If you’re looking for a tool to help you model dynamic, real-world systems where past events shape the future, Hawkes Processes are well worth your time.
I encourage you to explore the libraries we discussed, experiment with different kernels, and dive deeper into their applications in your field. The beauty of Hawkes Processes is that they provide a structured way to make sense of seemingly random, chaotic events—whether in markets, networks, or natural phenomena.
