What is Manifold Learning?
You know how sometimes it feels like everything is way more complicated than it needs to be? Well, data in machine learning is no different. Imagine you’ve got a dataset that looks like it lives in a high-dimensional space—kind of like trying to make sense of a tangled ball of yarn. But what if I told you that the underlying structure of that data is far simpler, existing on a smooth, lower-dimensional surface, or “manifold”? That’s what manifold learning is all about—finding this hidden simplicity in the chaos.
In simple terms, manifold learning is a set of techniques that help uncover the low-dimensional structure embedded in high-dimensional data. It’s often used for dimensionality reduction, where you want to reduce the number of variables in your dataset without losing important information. Imagine trying to simplify a 3D model into a flat image—while keeping all the key features intact. Manifold learning does this by finding the intrinsic geometry of the data.
For example, think of images of faces. While each pixel in an image could be treated as a separate dimension, the underlying structure (like where the eyes, nose, and mouth are positioned) follows a much simpler pattern. That’s the “manifold” the data lies on. And using manifold learning techniques, we can find that simpler structure.
What is the Wasserstein Space?
Now, let’s shift gears. Wasserstein space might sound like something straight out of sci-fi, but it’s rooted in some of the most elegant mathematics—optimal transport theory. Think of it this way: imagine you’re a transporter moving goods from one location to another, and you want to minimize the cost of transportation. How do you figure out the best way to do that?
The Wasserstein distance answers that question—but instead of moving goods, it measures how “different” two probability distributions are. It’s a way of comparing distributions by calculating the minimum effort required to transform one into the other. You can think of it as the “cost” of reshaping one pile of sand into another pile with a different shape and volume.
Wasserstein space, then, is the “landscape” in which these distributions live. When we talk about learning in this space, we’re moving beyond individual data points and diving into the world of probability distributions.
Why Combine Manifold Learning with Wasserstein Space?
Here’s the deal: most manifold learning methods focus on individual data points. But, what if your data is not a set of points but rather a collection of distributions? Enter the Wasserstein space, where distributions take center stage.
By combining manifold learning with Wasserstein space, you can study the underlying structure of probability distributions. This is particularly powerful for fields like generative models, where you’re not just interested in isolated data points, but the entire distributions they come from. For instance, in Wasserstein GANs, learning on distributions in Wasserstein space ensures smoother, more stable generative models. This can make a world of difference in applications like image generation or data augmentation.
The magic happens when you realize that this approach lets you smoothly interpolate between distributions—kind of like finding the shortest path between two cities on a map, except here you’re navigating between different statistical worlds. Recent advances in machine learning, particularly in generative models, have shown just how powerful this combination can be for building models that generate highly realistic data.
Foundations of Wasserstein Distance
Optimal Transport Theory
Let’s rewind a bit. The roots of Wasserstein distance are in optimal transport theory, which dates all the way back to the 18th century when a mathematician named Gaspard Monge started thinking about the most efficient way to move dirt around to build roads. In modern terms, think of it as finding the best way to transport mass from one place to another with minimal effort.
Imagine you’ve got two piles of sand—one representing a distribution of data points in one set and the other representing a different distribution. Your goal is to transform one pile into the other in the cheapest possible way. That’s optimal transport. The question of how to do this most efficiently is known as the Monge-Kantorovich problem.
In machine learning, we’re often dealing with probability distributions instead of physical piles of sand, but the concept is the same. You want to measure how different two distributions are by calculating the minimum cost required to transport one distribution into another. This is where the Wasserstein distance comes in.
Wasserstein Metric Definition
You might be wondering: how exactly do we compute this distance?
The Wasserstein distance (specifically the 1st and 2nd order distances) is a mathematical formula that computes the minimum effort required to turn one distribution into another. Here’s the general idea:
- First-order Wasserstein distance measures the “average” transportation cost.
- Second-order Wasserstein distance takes the variance of the data into account, giving more weight to outliers.
For two probability distributions P and Q, the Wasserstein distance W(p,q) is defined as:
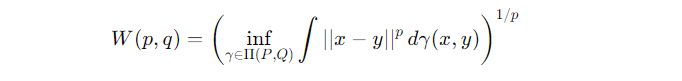
In this equation, γ\gammaγ represents a coupling between PPP and Q, and we’re minimizing over all possible ways to couple them. The resulting distance tells you how hard it would be to move P to Q, considering all possible ways to match up points between the two distributions.
Importance in Machine Learning
So why should you care about Wasserstein distance?
This metric has turned out to be extremely useful in machine learning, especially in generative models like Wasserstein GANs. In traditional GANs, the challenge is to minimize the difference between generated and real data, but the standard distance metrics can lead to instability. Wasserstein distance solves this by providing a smoother, more interpretable way to measure how different two distributions are.
The Wasserstein distance doesn’t just care about the values in the distributions—it takes into account the geometry of the data. This helps stabilize training and provides better feedback for the model, resulting in more realistic outputs. In fact, Wasserstein GANs have been shown to outperform traditional GANs in generating realistic images, and they’re more robust to issues like mode collapse.
By understanding how to apply the Wasserstein distance to your machine learning tasks, you can unlock better performance in probabilistic models, clustering algorithms, and, of course, manifold learning in Wasserstein space.
Manifold Learning Overview
Intrinsic Geometry of Data
Picture this: You’ve got a set of images, and each image is represented as a collection of thousands or even millions of pixel values. If you think about it, that’s a ridiculously high-dimensional space, right? Now, here’s the twist—despite these high dimensions, the actual meaningful structure of your data often lies on a much lower-dimensional surface or manifold. That’s the intrinsic geometry of data.
Let me give you an example to clarify. Imagine you’ve got a dataset of faces. Each image is a high-dimensional vector, but in reality, all these faces lie on a much simpler, low-dimensional manifold. Why? Because every face is just a variation of the same underlying structure—eyes, nose, mouth, etc. Manifold learning helps you figure out that the data, which appears to be trapped in a complex, high-dimensional space, actually lives on a more structured and simple surface.
Manifolds can also be thought of as a curved, smooth surface embedded in a higher-dimensional space. So, when you look at data in this context, it’s like trying to unfold or flatten a 3D object onto a 2D plane without losing its essential features. That’s where manifold learning techniques come in—to uncover the hidden simplicity in your data’s geometry.
Popular Manifold Learning Algorithms
You might be wondering: How do we actually do this manifold learning? Fortunately, we’ve got a set of powerful tools. Let me introduce you to a few popular ones:
- Isomap: Think of Isomap as a way to preserve the global geometry of the data. It builds a graph by connecting data points based on their nearest neighbors and then tries to preserve the shortest paths between them when reducing dimensions. It’s great when you need to preserve the overall structure of the data manifold.
- Locally Linear Embedding (LLE): Here’s a clever one—LLE is all about capturing the local geometry of data. It assumes that each data point can be approximated by a linear combination of its neighbors. By maintaining these relationships, LLE finds a low-dimensional embedding that reflects the local structure.
- t-SNE (t-distributed Stochastic Neighbor Embedding): If you’re into visualizing high-dimensional data, t-SNE is your go-to. It focuses on preserving the local neighborhood structure and works wonders for creating 2D or 3D visualizations that let you see the cluster patterns in your data.
Each of these methods has its own flavor, depending on whether you want to preserve global or local structures, or whether you need a method designed for visualization versus general dimensionality reduction. You’ve got options, but here’s the catch: none of these methods were originally designed to work with probability distributions.
Limitations of Traditional Manifold Learning
Here’s where things get tricky. Traditional manifold learning methods—like Isomap, LLE, and t-SNE—are fantastic when dealing with fixed data points. But when you move into the world of probability distributions, these methods start to show cracks.
Think about it: Traditional manifold learning algorithms assume that the input is a set of data points, not distributions. In many modern applications—especially when dealing with uncertain data or generative models—you’re more interested in how distributions relate to each other. Traditional methods don’t capture this complexity well. In other words, they miss out on the intricate relationships between distributions because they’re not equipped to handle the geometry of distributional spaces.
That’s where manifold learning in Wasserstein space comes into play. Let’s dive in.
Manifold Learning in Wasserstein Space
Extending Manifold Learning to Probability Distributions
This might surprise you: You don’t always deal with fixed data points in real-world applications. Sometimes, you’re working with entire distributions. The good news is that manifold learning can be extended to this case by leveraging the geometry of Wasserstein space.
Here’s the deal: Instead of treating your data as isolated points in space, you treat each data point as a probability distribution. In Wasserstein space, these distributions don’t float aimlessly; they live on a well-defined manifold with its own geometry. So, how do you measure distances between distributions? You use the Wasserstein distance, which we discussed earlier. This distance gives you the “cost” of transforming one distribution into another—sort of like mapping out the shortest path between two cities, but for statistical distributions.
By applying manifold learning techniques to Wasserstein space, you can uncover the underlying structure of these distributions. This opens up new dimensions of understanding, especially in fields where distributions, not just individual points, are crucial.
Applications of Manifold Learning in Wasserstein Space
Now let’s talk about where this gets really interesting—the applications.
Generative Models
One of the most exciting applications is in generative models like Wasserstein GANs (Generative Adversarial Networks) and Variational Autoencoders (VAEs). Here’s why this is important: Generative models don’t just learn from isolated data points; they aim to learn the entire distribution of the data. When you apply manifold learning in Wasserstein space, you’re allowing these models to better capture the underlying distributional structure, which leads to more realistic generations.
For example, in Wasserstein GANs, the generator learns to produce new data points by minimizing the Wasserstein distance between the real data distribution and the generated distribution. The result? More stable training and sharper, more realistic images. You’ve probably seen those incredible AI-generated images—yeah, that’s partly thanks to the power of Wasserstein-based learning.
Clustering in Distributional Spaces
Here’s another cool application: clustering. Traditional clustering methods (like k-means) assume that you’re working with fixed points, but what if you want to cluster distributions? That’s where clustering in Wasserstein space comes in. By using Wasserstein distance, you can cluster probability distributions themselves, which is particularly useful in fields like medical imaging or natural language processing. For example, you could cluster distributions of brain scan patterns or even textual representations in NLP models, which gives you deeper insights than clustering individual data points ever could.
Interpolation Between Distributions
And finally, let’s talk about interpolation. Say you’ve got two probability distributions, and you want to smoothly transition from one to the other. In traditional manifold learning, interpolating between two data points is simple—you just draw a line. But in Wasserstein space, interpolating between distributions is far more sophisticated. You’re not just shifting data points; you’re reshaping entire distributions, allowing for smooth, realistic transitions.
This has practical uses in areas like style transfer and data augmentation. Imagine you’re working with a dataset of different artistic styles, and you want to generate new styles by blending two existing ones. Manifold learning in Wasserstein space lets you smoothly interpolate between these styles, creating entirely new, yet coherent artistic pieces.
Mathematical Framework
Geodesics in Wasserstein Space
You might be wondering: What’s the shortest path between two distributions? In everyday geometry, we know the shortest path between two points is a straight line, right? Well, when we’re talking about Wasserstein space, things get a bit more intriguing.
In the world of probability distributions, the equivalent of a straight line is called a geodesic. It’s the shortest path between two distributions in Wasserstein space, just like the shortest path between two points on the surface of a sphere would be an arc (rather than a straight line). This geodesic isn’t just a theoretical curiosity—it actually tells us how to smoothly transform one probability distribution into another, which is critical when you’re trying to understand how distributions evolve or interpolate between them.
Geodesics play a vital role in understanding the structure of manifolds in Wasserstein space. Why? Because they help us define the “shape” of the space between distributions, guiding how we measure distances, interpolate, and make sense of the manifold. For example, in generative models, geodesics can represent the path along which new data points are generated, ensuring the process stays as smooth as possible.
Tangent Space Approximation
Let’s dive into another important concept: tangent spaces. In manifold learning, you’ll often hear about approximating complex, non-linear manifolds using tangent spaces—which are essentially flat, linear approximations of curved surfaces.
Think of it this way: You’re standing on a hill (the manifold), and you want to take a tiny step forward. Instead of worrying about the entire hill’s curvature, you can approximate your local environment with a flat surface (a tangent plane). This approximation is usually good enough for small steps, and that’s exactly how tangent spaces work in Wasserstein space.
At any given distribution, you can calculate the tangent space, which gives you a local linear approximation of the manifold. This allows you to apply traditional linear methods (like PCA or gradient-based optimization) locally while still navigating a non-linear space. Tangent spaces are incredibly useful when you need to perform local linear operations, such as computing gradients or conducting small-step optimizations, which are necessary for algorithms like Wasserstein PCA.
Manifold Learning Techniques in Wasserstein Space
Now, you’re probably curious about the actual algorithms used for manifold learning in Wasserstein space. Here are some of the key techniques:
- Wasserstein PCA: Just like regular PCA (Principal Component Analysis), Wasserstein PCA helps reduce the dimensionality of data, but it operates on probability distributions rather than fixed data points. By working in Wasserstein space, it accounts for the geometry of distributions, enabling you to find low-dimensional structures that are more meaningful when your data consists of distributions.
- Entropic Regularization Methods: One challenge with Wasserstein distance is that it can be computationally expensive. That’s where entropic regularization comes in, making the computation faster and more stable. This technique adds a small “entropy” term to the optimization problem, which smooths out the solution, making it easier to compute while still maintaining accuracy. It’s a clever trick that speeds up optimal transport calculations without losing too much precision.
- Stochastic Gradient-Based Approaches: Many learning tasks in Wasserstein space, especially those involving large datasets, rely on stochastic gradient-based optimization. These methods are ideal for minimizing the Wasserstein distance between distributions over time, which is useful in generative models or when training deep neural networks.
Each of these techniques allows us to handle probability distributions in a principled way, uncovering underlying manifold structures that are otherwise hidden in traditional point-based learning.
Case Studies and Examples
Example 1: Image Synthesis with Wasserstein GAN
Here’s a real-world application that’s going to blow your mind—image synthesis using Wasserstein GANs. Traditional GANs have been around for a while, but one of their biggest challenges is that they can be unstable during training, leading to issues like mode collapse (where the model only generates a limited variety of images). Enter Wasserstein GANs, which use the Wasserstein distance to smooth out the training process.
So, how does manifold learning in Wasserstein space help? In the case of image synthesis, the generator in a Wasserstein GAN learns to map random noise distributions to real-world image distributions. By using manifold learning in Wasserstein space, the generator can move along the geodesics between the noise distribution and the real image distribution, producing more realistic, high-quality images as a result.
Imagine training a model to generate lifelike portraits. Instead of just randomly guessing where new images might lie, the Wasserstein GAN navigates the distributional manifold, ensuring that each generated image is a realistic variation within the space of real human faces.
Example 2: Data Interpolation
Next up: data interpolation. Picture this: You’ve got two distinct distributions—maybe two different styles of artwork, or two sets of facial expressions—and you want to generate new data that smoothly transitions from one to the other. How do you do that? Manifold learning in Wasserstein space lets you compute geodesics between the two distributions, enabling you to interpolate smoothly between them.
In practical terms, this means you can blend two distributions and generate new data points that lie in between. For example, imagine smoothly transitioning between two different art styles or mixing two sets of patient data in a healthcare application. You’re no longer stuck with rigid transformations—you’ve got smooth, realistic interpolation that captures the full complexity of the data.
Example 3: Clustering Distributions in Healthcare Data
Finally, let’s look at clustering distributions in healthcare data. Suppose you’re working with medical images, like MRI scans or histograms of patient biometrics. Each image isn’t just a fixed data point—it represents a distribution of values (e.g., the distribution of pixel intensities). Traditional clustering algorithms won’t cut it here because they don’t account for the distributional nature of the data.
By applying manifold learning in Wasserstein space, you can cluster these distributions based on their geometric relationships. For example, you could group together MRI scans that show similar patterns of brain activity, even though the exact pixel values may differ. This enables more sophisticated grouping and diagnosis of patients, leading to insights that are otherwise hidden in traditional data analysis methods.
Conclusion
Let’s wrap things up. Manifold learning in Wasserstein space represents a fascinating and powerful fusion of two complex concepts: manifold learning, which helps you uncover the hidden geometric structure of your data, and Wasserstein space, where probability distributions themselves take center stage.
By combining these two, you open the door to solving some of the most challenging problems in modern machine learning—from generative modeling to data interpolation and clustering in distributional spaces. You’re no longer confined to static data points; instead, you’re operating in a world of distributions, with richer, more nuanced insights at your fingertips.
We explored how geodesics and tangent space approximation provide you with the mathematical tools to navigate this space, while techniques like Wasserstein PCA and entropic regularization help you handle the computations more efficiently. Whether you’re generating lifelike images with Wasserstein GANs, smoothly transitioning between datasets, or clustering distributions in healthcare applications, the manifold structure in Wasserstein space is your guide.
In a world where data is becoming more complex and probabilistic, mastering manifold learning in Wasserstein space equips you with the cutting-edge techniques needed to unlock new possibilities and gain deeper insights.
In the end, it’s not just about reducing dimensions—it’s about understanding the shape of your data, no matter how complex it may be. With these tools and insights, you’re ready to explore distributional manifolds and push the boundaries of what’s possible in machine learning.
