Let me ask you this: Have you ever built a regression model that seemed to fit your data perfectly, only to find out that it completely falls apart when faced with new, unseen data? If so, you’re not alone! This problem, known as overfitting, is one of the most common challenges in data science. But don’t worry, there’s a solution that might just change how you handle regression: Lasso Regression.
Overview:
Here’s the deal: Lasso Regression isn’t just another fancy algorithm—it’s a method that takes your standard regression model and adds a little something special called regularization. What does that mean for you? Well, instead of letting your model get too cozy with every feature in your dataset, Lasso helps to simplify things by shrinking some of those feature coefficients down to zero. Essentially, it’s like Marie Kondo for your regression model, tidying up irrelevant features so that only the most important ones remain.
In plain terms, Lasso is the shortcut to a model that not only fits your data but also generalizes well, helping you avoid the dreaded overfitting problem.
Why Lasso?
Now, you might be wondering, “Why should I use Lasso when there are so many other regression techniques out there?” Here’s why: Lasso isn’t just about regularization; it’s about feature selection. Unlike Ridge Regression, which shrinks coefficients but never truly eliminates them, Lasso goes a step further by setting some coefficients to exactly zero. This means Lasso isn’t just fine-tuning your model—it’s actively helping you choose which features to keep and which ones to drop.
Think of it this way: If you’re working with a dataset loaded with features, Lasso steps in like a seasoned detective, figuring out which clues (features) are truly relevant and which ones are just noise. And let’s be honest, we could all use a little help when things get too complex!
Steps to Build from Scratch:
1. Data Preparation:
First things first, we need data. Let’s say you’re using synthetic data (it’s always a good starting point when building models from scratch). For this, we’ll need a few key libraries: numpy for numerical operations, pandas for data handling, and matplotlib for visualizations.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Generate some synthetic data
np.random.seed(42)
X = np.random.rand(100, 3)
beta_true = np.array([1.5, 0, -2]) # True coefficients (with one feature zeroed out)
y = X @ beta_true + np.random.randn(100) * 0.1 # Linear relation with some noise
You might be wondering, “Why are we generating synthetic data?” Simple—it gives us complete control, so we can clearly see how Lasso zeroes out those unnecessary coefficients.
2. Loss Function:
The next step is to write the Lasso loss function. In standard linear regression, the loss function is just the sum of squared errors. With Lasso, we add the L1 regularization term, which penalizes large coefficients:
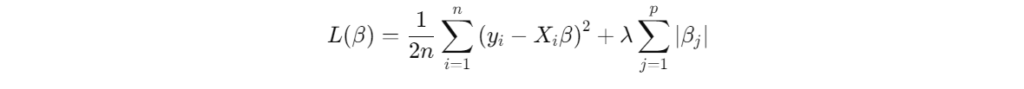
Here, λ\lambdaλ controls the strength of the regularization. A higher λ means more coefficients will be forced to zero.
Let’s translate that into code:
def lasso_loss(X, y, beta, lam):
n = len(y)
predictions = X @ beta
residuals = y - predictions
loss = (1 / (2 * n)) * np.sum(residuals ** 2) + lam * np.sum(np.abs(beta))
return loss
Now, every time you adjust β\betaβ, you’ll be penalizing the large values—this is the regularization effect kicking in.
3. Gradient Descent Implementation:
Here’s where things get interesting. To minimize the Lasso loss, we’ll use gradient descent. But Lasso’s L1 penalty makes things a little tricky: the gradient isn’t smooth. So, we have to implement a soft-thresholding operator to handle the L1 term.
Here’s how you might implement gradient descent for Lasso:
def lasso_gradient_descent(X, y, beta, lam, learning_rate, iterations):
n = len(y)
for _ in range(iterations):
predictions = X @ beta
gradient = -(1 / n) * X.T @ (y - predictions)
beta = beta - learning_rate * gradient
# Apply soft-thresholding for L1 regularization
beta = np.sign(beta) * np.maximum(0, np.abs(beta) - learning_rate * lam)
return beta
You might be thinking, “Why do we need soft-thresholding?” Good question! The L1 penalty isn’t smooth, so the soft-thresholding ensures that the coefficients are updated properly while some are shrunk to exactly zero.
4. Handling Shrinking Coefficients:
Here’s the deal: Lasso isn’t just about shrinking coefficients; it’s about setting them to zero. The soft-thresholding step in the gradient descent ensures that this happens. Essentially, if a coefficient’s absolute value is smaller than the regularization parameter λ, it gets set to zero. This is why Lasso is such an efficient tool for feature selection.
5. Regularization Parameter Tuning:
Let’s not forget about λ. You might be wondering, “How do I choose the right value for λ?” This is where things like cross-validation come into play. Typically, you’ll try several values of λ\lambdaλ and see which one leads to the best performance on validation data.
# Simple range of lambda values to test
lambdas = [0.01, 0.1, 1.0, 10.0]
By adjusting λ, you control how aggressively Lasso shrinks the coefficients. A small λ keeps most of the features, while a larger λ drops the irrelevant ones.
6. Code Walkthrough:
Finally, here’s the full implementation for Lasso Regression from scratch. I’ll walk you through the code and explain each step:
import numpy as np
# Lasso loss function
def lasso_loss(X, y, beta, lam):
n = len(y)
predictions = X @ beta
residuals = y - predictions
loss = (1 / (2 * n)) * np.sum(residuals ** 2) + lam * np.sum(np.abs(beta))
return loss
# Gradient descent with soft-thresholding
def lasso_gradient_descent(X, y, beta, lam, learning_rate, iterations):
n = len(y)
for _ in range(iterations):
predictions = X @ beta
gradient = -(1 / n) * X.T @ (y - predictions)
beta = beta - learning_rate * gradient
# Apply soft-thresholding
beta = np.sign(beta) * np.maximum(0, np.abs(beta) - learning_rate * lam)
return beta
# Generate synthetic data
np.random.seed(42)
X = np.random.rand(100, 3)
beta_true = np.array([1.5, 0, -2])
y = X @ beta_true + np.random.randn(100) * 0.1
# Initialize beta and parameters
beta_init = np.random.randn(3)
lambda_param = 0.1
learning_rate = 0.01
iterations = 1000
# Perform Lasso Regression
beta_hat = lasso_gradient_descent(X, y, beta_init, lambda_param, learning_rate, iterations)
print("Estimated coefficients:", beta_hat)
In this code, we start with a random initialization of the coefficients (beta_init), perform gradient descent with soft-thresholding, and finally print out the estimated coefficients. You’ll notice that some coefficients might shrink all the way to zero, depending on the value of
tical Example: Lasso Regression with Real Data
Dataset Introduction:
Let’s jump into some real-world data, shall we? You might be thinking, “Why is this important?” Well, using real-world data helps you see how Lasso works beyond synthetic examples—it shows how it handles the complexity of real-life scenarios.
For this example, I’ll use the famous Boston Housing dataset from scikit-learn. It’s widely known and easy to work with. The dataset contains information about housing prices in Boston, with features like crime rate, average number of rooms per dwelling, and more. The goal is to predict the median value of homes (our target variable) using these features.
But before diving in, preprocessing is crucial. Since Lasso is sensitive to feature scales (because of the L1 regularization), we need to make sure the features are scaled properly. This is where feature scaling comes in. You don’t want one feature dominating simply because it has larger values than others.
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# Load dataset
boston = load_boston()
X = boston.data
y = boston.target
# Split into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Feature scaling
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)See what I did there? I scaled the data to make sure each feature has the same weight in the model. You might be wondering why this matters—trust me, when it comes to regularization, scaled features make all the difference.
Implementation with Scikit-learn:
1. Fitting the Model:
Now that we’ve preprocessed the data, it’s time to fit the Lasso model using scikit-learn. This is where Lasso does its magic by shrinking those unnecessary coefficients to zero.
from sklearn.linear_model import Lasso
# Initialize Lasso model
lasso = Lasso(alpha=1.0) # alpha is the regularization strength (lambda in our earlier examples)
# Fit the model
lasso.fit(X_train_scaled, y_train)
# Predict on the test set
y_pred = lasso.predict(X_test_scaled)
# Evaluate the model
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")
The beauty of using scikit-learn is that it simplifies a lot of the heavy lifting. The alpha parameter here represents our regularization strength—just like λ\lambdaλ in our earlier implementation from scratch. A higher alpha means more regularization and, consequently, more coefficients will be forced to zero.
2. Hyperparameter Tuning:
Here’s where things get interesting. You might be thinking, “How do I choose the right value for α\alphaα?” Good question! The answer lies in cross-validation. Cross-validation helps you test multiple values of α\alphaα to see which one gives the best performance.
Let’s use scikit-learn’s GridSearchCV to find the optimal value:
from sklearn.model_selection import GridSearchCV
# Define a range of alpha values to test
alpha_range = [0.01, 0.1, 1, 10, 100]
# Set up grid search
lasso_cv = GridSearchCV(Lasso(), param_grid={'alpha': alpha_range}, cv=5)
lasso_cv.fit(X_train_scaled, y_train)
# Best alpha value
best_alpha = lasso_cv.best_params_['alpha']
print(f"Optimal alpha: {best_alpha}")
Now, you’re not just picking a random value for α\alphaα. You’re using cross-validation to find the sweet spot, ensuring your model performs well without underfitting or overfitting.
3. Feature Selection Example:
Here’s the fun part—feature selection. Lasso doesn’t just fit a model; it’s smart enough to know which features are pulling their weight and which ones are just dead weight. Let’s look at how Lasso automatically selects the most important features by shrinking irrelevant ones to zero.
# Get the coefficients
lasso_coefficients = lasso_cv.best_estimator_.coef_
# Print out the coefficients for each feature
print("Lasso coefficients:", lasso_coefficients)
This might surprise you: some of these coefficients will be exactly zero, meaning Lasso has determined that those features aren’t contributing much to the prediction. This is the power of Lasso—it’s not just regression, it’s feature selection in action.
Interpretation of Results:
1. Feature Importance:
So, how do you interpret the results? It’s all about those coefficients. The features with non-zero coefficients are the ones that Lasso has deemed important. In the Boston Housing dataset, for example, features like the number of rooms per dwelling (RM) or the proportion of non-retail business acres per town (INDUS) might stick around, while others like B (proportion of African Americans by town) might be reduced to zero.
Here’s what you do: focus on the non-zero coefficients. Those are your important features. The zeroed-out ones? They’re noise—Lasso has effectively filtered them out.
2. Comparison with Ridge and OLS:
Now, you might be wondering, “How does Lasso compare to Ridge and OLS?” Let’s break it down:
- OLS (Ordinary Least Squares): Fits the data as-is, with no regularization. It’s the go-to method when you believe all your features are important, but it tends to overfit when there are too many irrelevant features.
- Ridge Regression: Applies L2 regularization. This shrinks the coefficients but doesn’t set any to zero. It’s great when you have multicollinearity (features that are highly correlated), but it doesn’t do feature selection.
- Lasso Regression: Uses L1 regularization, and here’s the kicker—it actually sets some coefficients to zero, performing automatic feature selection. This makes it perfect for high-dimensional datasets where you suspect many features are irrelevant.
So, if you have a lot of irrelevant features, Lasso is your friend. But if your features are all equally important and there’s multicollinearity, Ridge might be a better choice.
3. When to Use Lasso:
Here’s the bottom line: Lasso is perfect when you’re working with high-dimensional data (lots of features) and suspect that many of those features aren’t really contributing much. It’s also great when you want your model to be interpretable, as Lasso will reduce the number of features, making it easier to understand which ones actually matter.
If you’ve got a large dataset with many irrelevant features, Lasso is your go-to. But if your features are all critical and you just want to avoid overfitting, Ridge might be a better fit.
Conclusion:
Lasso Regression isn’t just another tool in your machine learning toolkit—it’s a powerful technique that combines regression with feature selection. By applying L1 regularization, Lasso shrinks the coefficients of irrelevant features to zero, helping you build simpler, more interpretable models. Whether you’re working with a high-dimensional dataset or simply looking to prevent overfitting, Lasso is a solid choice that helps you cut through the noise and focus on what truly matters.
